In this guide, I am going to show you how to activate windows 10 for free permanently in 2021.
In fact, it is totally free to activate windows 10 using this method and you do not require any product key or activation key.
It works for any Windows 10 Edition including:
- Windows 10 Home
- Windows 10 Home N
- Windows 10 Home Singe Language
- Windows 10 Professional
- Windows 10 Professional N
- Windows 10 Education N
- Windows 10 Enterprise
- Windows 10 Enterprise N
The best part?
You can do it in just 2 minutes!
Table of Contents
How To Activate Windows 10 For Free Permanently With CMD
This method involved the use of your command prompt (CMD). Here’s how to go about it.
I have created a video guide for this, you can watch the video below:
Step 1. Run CMD As Administrator
- In your windows search, type CMD
- Click on Run as Administrator as seen below.
Or you can right click on Command Prompt and select Run as administrator as seen below.
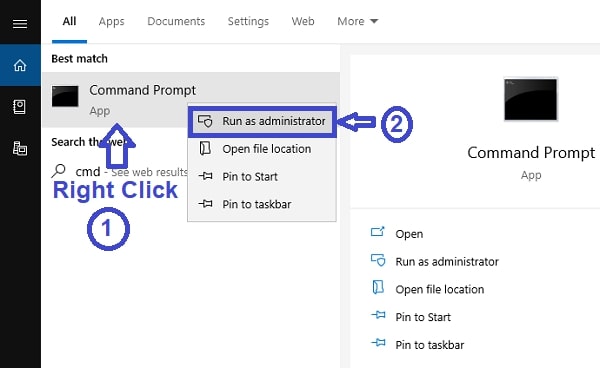
Either ways, your command prompt will open.
Step 2. Install KMS Client key
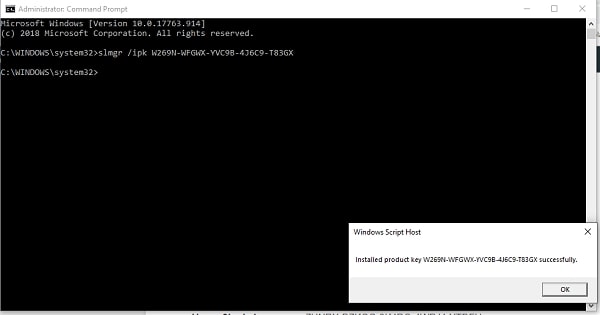
Enter the command slmgr /ipk yourlicensekey and click Enter button on your keyword to execute the command.
The following is the list of Windows 10 Volume license keys.
Home: TX9XD-98N7V-6WMQ6-BX7FG-H8Q99
Home N: 3KHY7-WNT83-DGQKR-F7HPR-844BM
Home Single Language: 7HNRX-D7KGG-3K4RQ-4WPJ4-YTDFH
Home Country Specific: PVMJN-6DFY6-9CCP6-7BKTT-D3WVR
Professional: W269N-WFGWX-YVC9B-4J6C9-T83GX
Professional N: MH37W-N47XK-V7XM9-C7227-GCQG9
Education: NW6C2-QMPVW-D7KKK-3GKT6-VCFB2
Education N: 2WH4N-8QGBV-H22JP-CT43Q-MDWWJ
Enterprise: NPPR9-FWDCX-D2C8J-H872K-2YT43
Enterprise N: DPH2V-TTNVB-4X9Q3-TJR4H-KHJW4
For example, if you are using Windows 10 Education, enter command slmgr /ipk NW6C2-QMPVW-D7KKK-3GKT6-VCFB2 as seen below.
Step 3. Activate Windows
After installing the KMS client key, the next thing is to activate windows for free using CMD prompt.
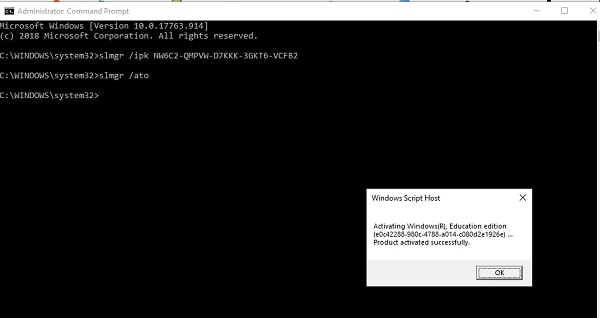
- On the next line, enter the code slmgr /ato as seen below.
- Click Enter to execute the command and your windows will be activated immediately.
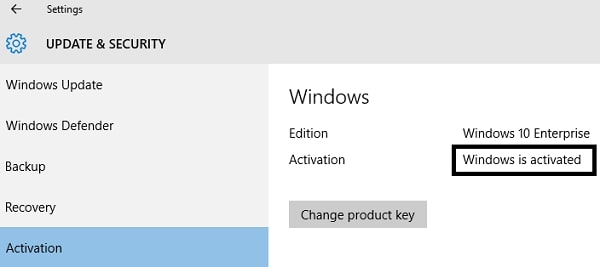
Now, you can confirm that your Windows has been activated successfully.
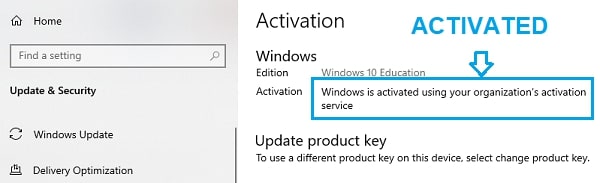
Go to Settings >> Activation.
I’m sure this method will work for you, don’t forget to drop a comment below and share.
Free Windows 10 Activators (Works 100%)
There is another method to activate your Windows 10 using free activators.
The best activators I tried and are working very well are:
- Microsoft Toolkit
- KMSPico
You know the best part?
You do not need to keep these software after use.
Even when you uninstall them, your Windows will be remain activated.
Now, I will show you how to use each Windows activator easily.
Windows Activator 1 – KMSPico
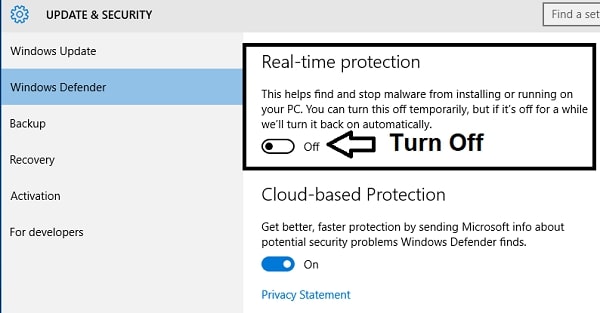
- Also, you need to disable Real Time Protection under the Windows Defender Settings.
- Now, download KMSPico software by clicking here.
- Unzip and install the software (Password is 12345)
- Open the software after Installation.
- Once the software opens, click on the Red button and your Windows 10 will be activated immediately!
Windows Activator 2 – Microsoft Toolkit
First, you need to temporarily disable Anti-virus and Windows Defender Protection (this is necessary because the antivirus will not allow Microsoft Toolkit to modify system registry which is needed to activate Windows).
- Search for Windows Defender Settings and click on it
- Turn off Real Time Protection
- Next, download Microsoft Toolkit by clicking here.
- Unzip the file and Install it. (Password is 123)
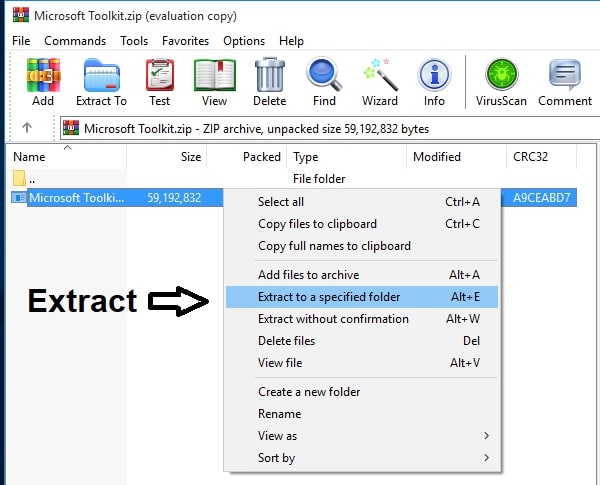
- Open the software and click on the Windows icon beside the Settings button in the software
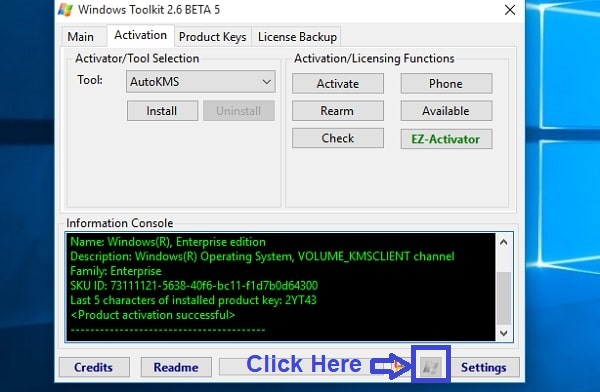
- Click on Product Keys tab and select the Product and Edition (e.g Windows 10 Professional). Click on Install.
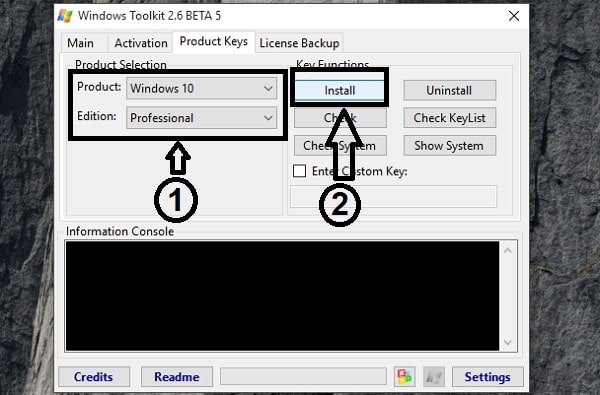
- Now, go to the Activation tab, select KMS Server Service and click Install.
- Finally, click on Activate. Your Windows will be activated immediately.
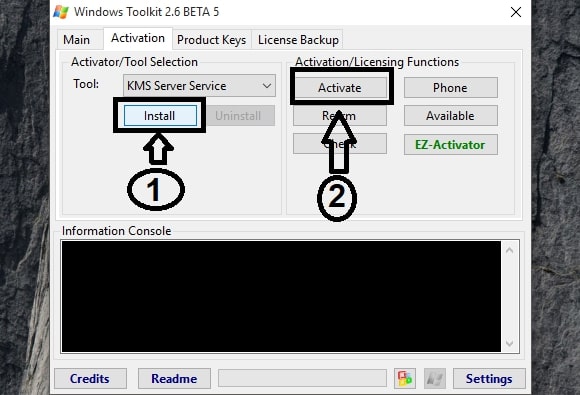
- If that doesn’t work, click on E-Z Activator.
How Not To Activate Windows 10
Although this method will also help you to activate your Windows 10 easily, I do not recommend it.
It involves the use of .bat file
- First, copy the code below:
The server in the code might have access to your computer, and that is why I do not recommend this method of activation
Your system might detect it as a virus and remove it (one of the reasons why I DO NOT recommend this method).
- Save the file as activator.bat and pick All files as the file type.
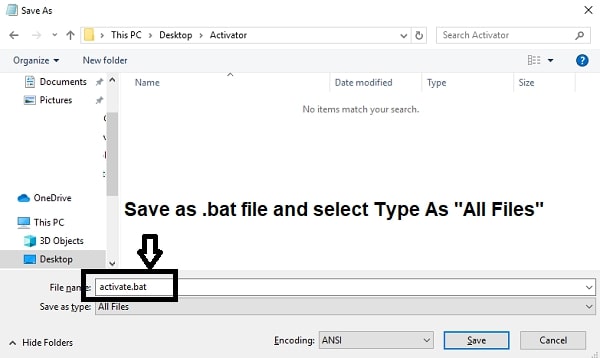
- Right Click on the file and Run as Administrator
- Wait for the Command Prompt to complete running the code.
- When you receive the message whether to restart PC, enter Y and click Enter.
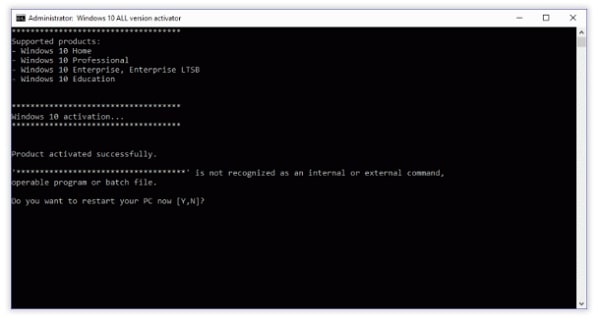
- Your PC will restart and your Windows will be activated.
Conclusion
I believe by now, you have been able to activate your Windows 10 for free without using any product key.
Personally, I used the first method to activate my Windows 10 in 2021 for free without activator or key.
Let me know which method you prefer by using the comment section below. Also, don’t forget to share the article by using the buttons below.



81 Comments
Leave a Reply